B@Z&RK neural network pages, Backpropagation neural network C++ source code by Thomas Riga, University of Genoa, Italy, keywords: neural networks, backpropagation, machine learning, neurocomputing, C++ source code, subsymbolism, connectionism, neuroscience, cognitive science

::: Neural networks :::

Although neural networks are inspired on the architecture of our brain, people who create these networks are well aware that they are not an accurate model of our brain. Nevertheless, these networks and our brain have in common:

massive parallelism
capacity to acquire knowledge and integrate it in the previously acquired knowledge
distribution of computation on many processing units, which have multiple purposes (one network can perform various tasks)
no division between processing units and memory containing knowledge
the processing units are massively interconnected
flexibility and unsensivity to malfunctioning of parts
capacity of association of patterns related, classification and generalization of them
they contain implicit representations of the relations between patterns, distributed on multiple units and connections

Classic AI works with explicit procedures to imitate human reasoning, and they focus on more sophisticated aspects of it. Neural networks focus more on low level functions of our reasoning. The general idea is that higher levels of our reasoning are based on low level aspects of it, and therefore, if we start simulating these low level aspects, eventually we will arrive to a theory which explains our reasoning in general.There exist many different architectures and learning algorithms for neural networks, one good example is the backpropagation algorithm.

Backpropagation

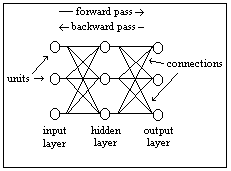backprop network A backpropagation network uses a supervised learning algorithm. An input pattern is presented to the network and then an output pattern is computed. This output pattern is compared to a target output pattern resulting in an error value. The error value is propagated backwards through the network, (the network inherits its name from this methodology) and the values of the connections between the layers of units are adjusted in a way that the next time the output pattern is computed, it will be more similar to the target output pattern. This process is repeated until output pattern and target output pattern are (almost) equal. A typical learning process involves a lot of couples of input and target output patterns, called cases. Backpropagation networks are useful, among other tasks, for classification and generalization. A good example of an implementation of these networks is character recognition. The ideators of the backpropagation algorithm compiled two volumes which sometimes are considered the bible of neural networks: Parallel distributed processing: Explorations in the microstructure of cognition, J.L. McLelland, D.E. Rumelhart and the PDP research group, MIT press/Bradford Books, 1986

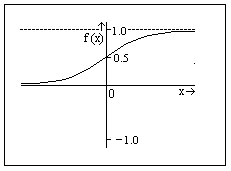Sigmoid function

The graphic on the left shows the sigmoid function for the units in the network. It is an exponential function which has as a most important characteristic the fact that, even if x assumes values next to the infinitely big or little, f(x) will assume a value between 0 and 1. The learning algorithm will adjust the weights of the connections between units so that the function translates values of x to a binary value, typically: f( x) > 0.9 : f(x) = 1 , f(x) < 0.1 : f(x) = 0.

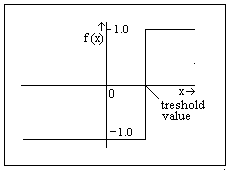Treshold function

An alternative used in networks for the sigmoid function is the treshold function which is shown in the graphic on the left. The output assumes just two values: -1 or 1. Some treshold functions have a binary output: 0 or 1. This function is less complex to compute when a network is implemented on a digital computer than the sigmoid function, but it is not useful in a backpropagation algorithm. An example of a network that uses a treshold function is the Boltzmann machine.

Batch training and on-line training

There are two basic types of learning: batch and on-line. Most neural networks use a hybrid combination: pattern learning.

Batch learning is associated with a finite design set of cases. Weight updates are accumulated after the presentation of each design case. However, the updates are not applied until all cases have been presented. This determines the end of an epoch. Then the process is repeated until a stopping criterion is satisfied. The state of the network at any time does not depend on the order in which the design cases are presented.

On-line learning was originally associated with a stream of random design inputs over which the designer had little control. Weight updates are applied immediately after each design case is presented. The process continues until a stopping criterion is satisfied. The state of the network at any time does depend on the order in which the design cases were presented. The length of an epoch is at the discretion of the designer (e.g., test the stopping criterion every N cases). Pattern learning is on-line learning recursively applied to a finite design set of N cases. It is prudent to randomize the order in which design cases are presented each epoch. It is possible to use batch learning in the on-line random stream scenario. It is also possible to alternate batch learning with on-line learning.

[next page] [index] [mail me]
Thomas Riga, University of Genoa, Italy