Sigmoid function
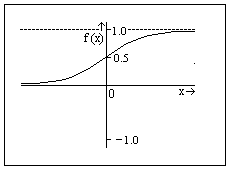 The graphic on the left shows the sigmoid function for the units in the network. It is an
exponential function which has as a most important characteristic the fact that, even if x
assumes values next to the infinitely big or little, f(x) will assume a value between 0 and 1.
This characteristic implies that the function translates values of x to a binary value, typically:
f( x) > 0.9 : f(x) = 1 , f(x) < 0.1 : f(x) = 0.
The graphic on the left shows the sigmoid function for the units in the network. It is an
exponential function which has as a most important characteristic the fact that, even if x
assumes values next to the infinitely big or little, f(x) will assume a value between 0 and 1.
This characteristic implies that the function translates values of x to a binary value, typically:
f( x) > 0.9 : f(x) = 1 , f(x) < 0.1 : f(x) = 0.
Treshold function
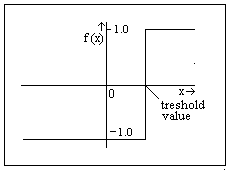 An alternative used in networks for the sigmoid function is
the treshold function which is shown in the graphic on the left.
The output assumes
just two values: -1 or 1. Some treshold functions have a binary
output: 0 or 1. This function is less complex to compute when a
network is implemented on a digital computer than the sigmoid
function, but it is not useful in a backpropagation algorhythm.
An alternative used in networks for the sigmoid function is
the treshold function which is shown in the graphic on the left.
The output assumes
just two values: -1 or 1. Some treshold functions have a binary
output: 0 or 1. This function is less complex to compute when a
network is implemented on a digital computer than the sigmoid
function, but it is not useful in a backpropagation algorhythm.
The PDP researchers
They are the ideators of the backpropagation algorhythm:
Parallel distributed processing: Explorations in the microstructure of cognition,
J.L. McLelland, D.E. Rumelhart and the PDP research group,
MIT press/Bradford Books, 1986
Thomas Riga, University of Genoa, Italy
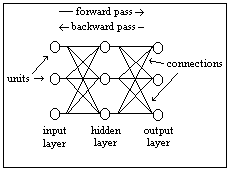 A backpropagation network uses a supervised learning algorhythm. An input pattern is
presented to the network and then an output pattern is computed. This output pattern is
compared to a target output pattern resulting in an error value. The error value is propagated
backwards through the network, (the network inherits its name from this methodology) and the
values of the connections between the layers of units are adjusted in a way that the next time
the output pattern is computed, it will be more similar to the target output pattern. This process
is repeated until output pattern and target output pattern are (almost) equal. A typical learning
process involves a lot of couples of input and target output patterns, called cases.
Backpropagation networks are useful, among other tasks, for classification and generalization.
A good example of an implementation of these networks is character recognition.
A backpropagation network uses a supervised learning algorhythm. An input pattern is
presented to the network and then an output pattern is computed. This output pattern is
compared to a target output pattern resulting in an error value. The error value is propagated
backwards through the network, (the network inherits its name from this methodology) and the
values of the connections between the layers of units are adjusted in a way that the next time
the output pattern is computed, it will be more similar to the target output pattern. This process
is repeated until output pattern and target output pattern are (almost) equal. A typical learning
process involves a lot of couples of input and target output patterns, called cases.
Backpropagation networks are useful, among other tasks, for classification and generalization.
A good example of an implementation of these networks is character recognition.